Expected Values-Variance,Co Variance and Correlation
The Expected Value of a Random Variable
The concept of the expected value of a random variable parallels the notion of a weighted average. The possible values of the random variable are weighted by their probabilities, as specified in the following definition.
$E(X)$ is also referred to as the mean of $X$ and is often denoted by $μ$ or $μX$ . It might be helpful to think of the expected value of $X$ as the center of mass of the frequency function. Imagine placing the masses $p(x_i )$ at the points $x_i$ on a beam; the balance point of the beam is the expected value of $X$.
The definition of expectation for a continuous random variable is a fairly obvious extension of the discrete case—summation is replaced by integration.
We often need to find E[g(X)], where X is a random variable and g is a fixed function
Now suppose that $Y = g(X1, . . . , Xn)$, where $Xi$ have a joint distribution, and that we want to find $E(Y )$. We do not have to find the density or frequency function of $Y$ , which again could be a formidable task.
We note the following immediate consequence of Theorem B.
COROLLARY A
If $X$ and $Y$ are independent random variables and $g$ and $h$ are fixed functions, then $E[g(X)h(Y )] = {E[g(X)]}{E[h(Y )]}$, provided that the expectations on the right-hand side exist. ■
In particular, if $X$ and $Y$ are independent, $E(XY) = E(X)E(Y )$.
Variance and Standard Deviation
The expected value of a random variable is its average value and can be viewed as an indication of the central value of the density or frequency function. The expected value is therefore sometimes referred to as a location parameter. The median of a distribution is also a location parameter, one that does not necessarily equal the mean. This section introduces another parameter, the standard deviation of a random variable, which is an indication of how dispersed the probability distribution is about its center, of howspread out on the average are the values of the random variable about its expectation.We first define the variance of a random variable and then define the standard deviation in terms of the variance.
If $X$ is a discrete random variable with frequency function $p(x)$ and expected value μ = E(X), then according to the definition
$Var(X)=\sum_i ( x_i - \mu)^2 p(x_i)$
whereas if $X$ is a continuous random variable with density function $f (x)$ and $E(X) = μ$
$Var(X)=\int_{- \infty}^{\infty} (x - \mu)^2 f(x) dx $
The variance is often denoted by $σ^2$ and the standard deviation by $σ$. From the preceding definition, the variance of $X$ is the average value of the squared deviation of $X$ from its mean. If $X$ has units of meters, for example, the variance has units of meters squared, and the standard deviation has units of meters.Although we are often interested ultimately in the standard deviation rather than the variance, it is usually easier to find the variance first and then take the square root.
The variance of a random variable changes in a simple way under linear transformations.
This result seems reasonable once you realize that the addition of a constant does not affect the variance, since the variance is a measure of the spread around a center and the center has merely been shifted.
The standard deviation transforms in a naturalway: $σ_Y = |b|σ_X$ . Thus, if the units of measurement are changed from meters to centimeters, for example, the standard deviation is simply multiplied by 100.
The following theorem gives an alternative way of calculating the variance
According to Theorem B, the variance of $X$ can be found in two steps: First find $E(X)$, and then find $E(X^2)$.
Covariance and Correlation
The variance of a random variable is a measure of its variability, and the covariance of two random variables is a measure of their joint variability, or their degree of association.After defining covariance, we will develop some of its properties and discuss a measure of association called correlation, which is defined in terms of covariance
The covariance is the average value of the product of the deviation of $X$ from its mean and the deviation of $Y$ from its mean. If the random variables are positively associated—that is, when $X$ is larger than its mean, $Y$ tends to be larger than its mean as well—the covariance will be positive. If the association is negative—that is, when $X$ is larger than its mean, $Y$ tends to be smaller than its mean—the covariance is negative. These statements will be expanded in the discussion of correlation.By expanding the product and using the linearity of the expectation, we obtain an alternative expression for the covariance,
$Cov(X, Y ) = E(XY − XμY − YμX + μXμY )$
$= E(XY) − E(X)μY − E(Y )μX + μXμY$
$= E(XY) − E(X)E(Y )$
In particular, if $X$ and $Y$ are independent, then $E(XY)= E(X)E(Y )$ and $Cov(X, Y ) =0$ (but the converse is not true)
We will now develop an expression for the covariance of linear combinations of random variables, proceeding in a number of small steps. First, since
$E(a + X) = a + E(X),$
$Cov(a + X, Y ) = E{[a + X − E(a + X)][Y − E(Y )]}$
$= E{[X − E(X)][Y − E(Y )]}$
$= Cov(X, Y )$
Next, since $E(aX) = aE(X),$
$Cov(aX, bY ) = E{[aX − aE(X)][bY − bE(Y )]}$
$= E{ab[X − E(X)][Y − E(Y )]}$
$= abE{[X − E(X)][Y − E(Y )]}$
$= ab Cov(X, Y )$
Next, we consider $Cov(X, Y + Z)$:
$Cov(X, Y + Z) = E([X − E(X)]{[Y − E(Y )] + [Z − E(Z)]})$
$= E{[X − E(X)][Y − E(Y )] + [X − E(X)][Z − E(Z)]}$
$= E{[X − E(X)][Y − E(Y )]}$
$+ E{[X − E(X)][Z − E(Z)]}$
$= Cov(X, Y ) + Cov(X, Z)$
We can now put these results together to find $Cov(aW + bX, cY + dZ):$
$Cov(aW + bX, cY + dZ) = Cov(aW + bX, cY ) + Cov(aW + bX, dZ)$
$= Cov(aW, cY ) + Cov(bX, cY ) + Cov(aW, dZ)+ Cov(bX, dZ)$
$= ac Cov(W, Y ) + bc Cov(X, Y ) + ad Cov(W, Z)+ bd Cov(X, Z)$
In general, the same kind of argument gives the following important bilinear property of covariance.
Note that because of the way the ratio is formed, the correlation is a dimensionless quantity (it has no units, such as inches, since the units in the numerator and denominator cancel). From the properties of the variance and covariance that we have established, it follows easily that if $X$ and $Y$ are both subjected to linear transformations (such as changing their units from inches to meters), the correlation coefficient does not change. Since it does not depend on the units of measurement, $ρ$ is in many cases a more useful measure of association than is the covariance.
The following notation and relationship are often useful. The standard deviations of $X$ and $Y$ are denoted by $σ_X$ and $σ_Y$ and their covariance by $σ_{XY}$ . We thus have
$ρ = \frac{σ_{XY}}{σ_Xσ_Y}$














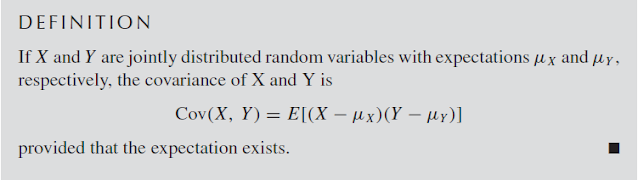





Comments
Post a Comment